🌻 JAVA/알고리즘, 자료구조
알고리즘 - 재귀 알고리즘 (feat. Factorial, Fibonacci)
iseunghan
2020. 11. 16. 17:02
반응형
재귀(Recursion) 이란 무엇일까?
어느 한 컴퓨터공학과 학생이 유명한 교수님을 찾아가 물었다.
"재귀함수가 뭔가요?"
"잘 들어보게. 옛날옛날 한 산 꼭대기에 이세상 모든 지식을 통달한 선인이 있었어. 마을 사람들은 모두 그 선인에게 수많은 질문을 했고, 모두 지혜롭게 대답해 주었지. 그의 답은 대부분 옳았다고 하네.
그런데 어느 날, 그 선인에게 한 선비가 찾아와서 물었어."재귀함수가 뭔가요?"
"잘 들어보게. 옛날옛날 한 산 꼭대기에 이세상 모든 지식을...
출처 : namu.wiki/w/%EC%9E%AC%EA%B7%80%ED%95%A8%EC%88%98
팩토리얼로 알아보는 재귀 알고리즘
먼저 팩토리얼 이란?
숫자 n이 주어졌을 때, n 부터 1까지의 곱의 결과를 뜻한다.
0! = 1
1! = 1
2! = 2 x 1
3! = 3 x 2 x 1
..
n! = n x (n-1) x ... x 1
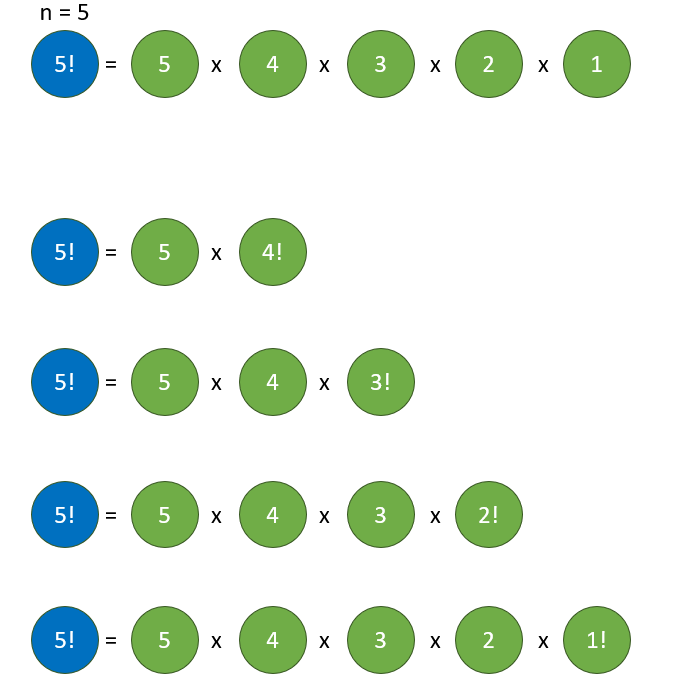
이것을 트리 형태로 만들면, 아래의 그림과 같다.
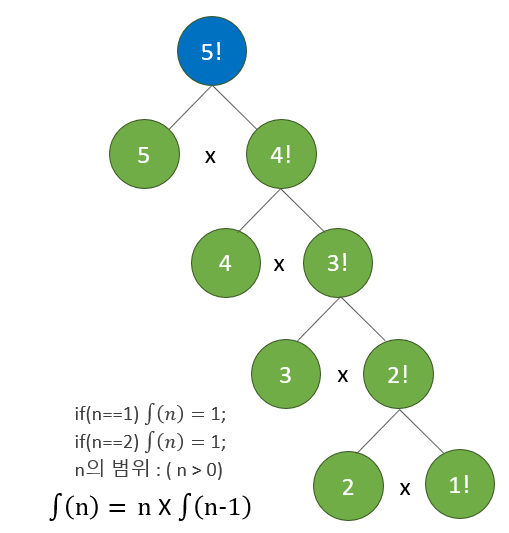
자 그럼 이제 점화식이 보인다.
if (n==1) 일 경우 ∫(n) = 1;
if (n==2) 일 경우 ∫(n) = 1;
n은 0보다 큰 양의 정수이다.
∫(n)= n x ∫(n-1)
코드로 표현 해보자.
import java.util.Scanner;
public class Factorial_10872 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int result = factorial(N);
System.out.println(result);
}
private static int factorial(int n) {
if (n == 0) {
return 1;
}
if (n == 1) {
return 1;
}
return n * factorial(n - 1);
}
}
피보나치로 알아보는 알고리즘
피보나치 수열이란?

출처 : ko.wikipedia.org/wiki/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98_%EC%88%98
피보나치 수열을 한번 자세히 보자.
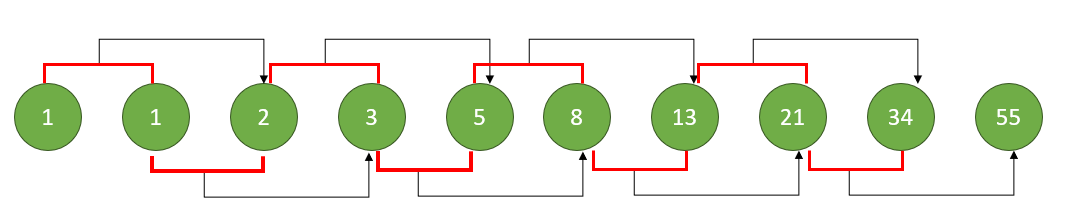
점화식을 작성 해 보자.
if(n==0 ) 일때, ∫(0) = 0;
∫(1) = 1;
∫(2) = 1;
n > 2 를 만족하는 양의 정수에 대하여
∫(n)= ∫(n-1) + ∫(n-2)
코드로 작성하면,
import java.util.Scanner;
public class Fibonacci {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int result = fibonacci(N);
System.out.println(result);
}
private static int fibonacci(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
if (n == 2) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
반응형