반응형
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
✏️ 문제
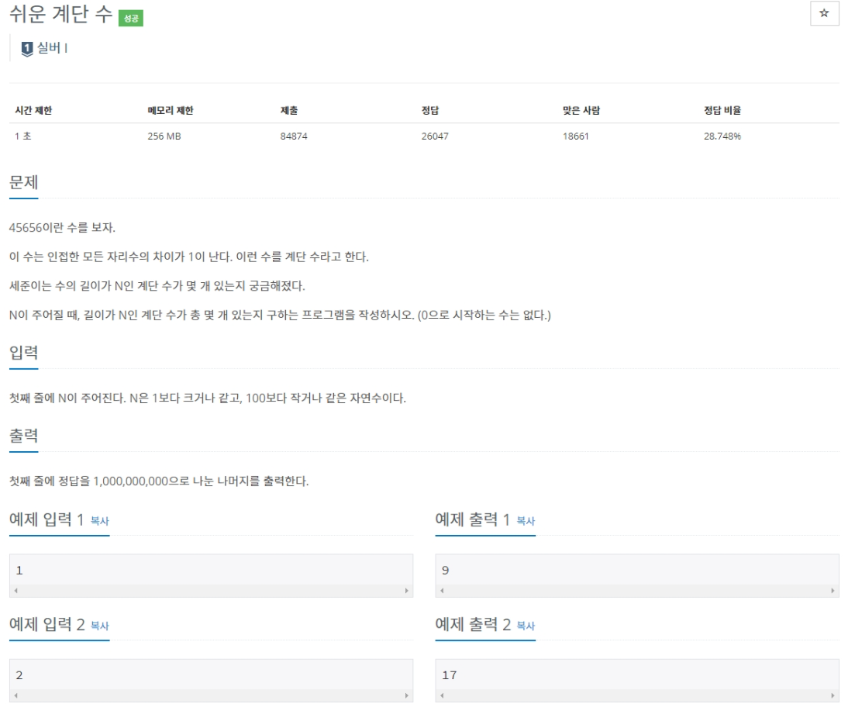
🔐 문제 해결
1. 테이블 정의
dp[i][j]는 길이가 i이고, j로 시작하는 수들 중 계단 수의 개수를 뜻합니다.
설명이 부족한 듯 해보여 아래의 표 형태로 표현해보았습니다.

- 0으로 시작하는 수는 없다고 조건에 나와있지만, 점화식을 세우기 위해서는 0으로 시작하는 계단 수도 필요합니다.
- dp[i][j]에는 위 표에서 정의한 대로 개수가 들어갈 것입니다. 여기서 중요한 포인트는 dp[1][0] = 0이라고 해서 개수가 0이 아닙니다! 1개로 체크해줘야 아래 점화식이 성립합니다.
2. 점화식 세우기
위 표를 참고하면서 점화식을 세우면 아래와 같습니다. (단, i는 2부터 시작합니다.)
- 길이가 i일 때, 0으로 시작하는 수는
dp[i][0]은dp[i-1][1]값과 동일합니다. (dp[i][j]는 개수입니다.) - 길이가 i이고 j로 시작하는 수 일때,
dp[i][j]는dp[i-1][j-1] + dp[i-1][j+1]과 동일합니다. - 단, 길이가 i이고 9로 시작하는 수는 dp[i-1][8]과 동일합니다.
위 조건을 코드로 나타내면 아래와 같습니다.
for(int i = 2; i <= N; i++) {
// 0으로 시작하는 계단 수의 개수는 길이가 i-1이고 1로 시작하는 계단 수의 개수와 동일합니다.
dp[i][0] = dp[i-1][1];
// j(1 ~ 8)로 시작하는 계단 수는 i-1길이의 j-1로 시작하는 계단 수와 j+1로 시작하는 계단수의 개수의 합과 동일합니다.
for(int j=1; j<=8; j++) {
dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1];
}
// 9로 시작하는 계단 수는 i-1길이의 8로 시작하는 계단 수의 개수와 같습니다.
dp[i][9] = dp[i-1][8];
}3. 초기값 설정
초기값으로는 길이가 1일 때의 계단 수의 개수만 설정해주면 됩니다.
주의해야 할 점은, int형 범위를 넘을 수 있기 때문에 long 배열을 사용합니다.
for(int i=0; i<=9; i++) {
dp[1][i] = 1L;
}
🗝 전체 코드
import java.io.*;
import java.util.*;
public class Main {
static int N;
static final long MOD = 1_000_000_000L;
public static void main(String args[]) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(bf.readLine());
long[][] dp = new long[N+1][10];
// init
for(int i=0; i<=9; i++) {
dp[1][i] = 1L;
}
for(int i=2; i<=N; i++) {
// 0으로 시작하는 수의 개수
dp[i][0] = dp[i-1][1];
for(int j=1; j<=9; j++) {
// 9일경우는 이전 자릿수의 8로 시작하는 수의 개수와 동일하다!
if(j == 9) dp[i][9] = dp[i-1][8] % MOD;
// 나머지 수들은 이전 숫자의 j-1로 시작하는 수의 개수와 j+1로 시작하는 수의 개수를 더한 값이다.
else dp[i][j] = (dp[i-1][j-1] % MOD + dp[i-1][j+1] % MOD) % MOD;
}
}
long result = 0;
for(int i=1; i<=9; i++) {
result = (result + dp[N][i]) % MOD; // 정답을 더하면서 오버플로우가 발생할 수 있으므로 주의!
}
System.out.print(result);
}
}감사합니다!
반응형
반응형
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
✏️ 문제

🔐 문제 해결
1. 테이블 정의
dp[i][j]는 길이가 i이고, j로 시작하는 수들 중 계단 수의 개수를 뜻합니다.
설명이 부족한 듯 해보여 아래의 표 형태로 표현해보았습니다.

- 0으로 시작하는 수는 없다고 조건에 나와있지만, 점화식을 세우기 위해서는 0으로 시작하는 계단 수도 필요합니다.
- dp[i][j]에는 위 표에서 정의한 대로 개수가 들어갈 것입니다. 여기서 중요한 포인트는 dp[1][0] = 0이라고 해서 개수가 0이 아닙니다! 1개로 체크해줘야 아래 점화식이 성립합니다.
2. 점화식 세우기
위 표를 참고하면서 점화식을 세우면 아래와 같습니다. (단, i는 2부터 시작합니다.)
- 길이가 i일 때, 0으로 시작하는 수는
dp[i][0]은dp[i-1][1]값과 동일합니다. (dp[i][j]는 개수입니다.) - 길이가 i이고 j로 시작하는 수 일때,
dp[i][j]는dp[i-1][j-1] + dp[i-1][j+1]과 동일합니다. - 단, 길이가 i이고 9로 시작하는 수는 dp[i-1][8]과 동일합니다.
위 조건을 코드로 나타내면 아래와 같습니다.
for(int i = 2; i <= N; i++) {
// 0으로 시작하는 계단 수의 개수는 길이가 i-1이고 1로 시작하는 계단 수의 개수와 동일합니다.
dp[i][0] = dp[i-1][1];
// j(1 ~ 8)로 시작하는 계단 수는 i-1길이의 j-1로 시작하는 계단 수와 j+1로 시작하는 계단수의 개수의 합과 동일합니다.
for(int j=1; j<=8; j++) {
dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1];
}
// 9로 시작하는 계단 수는 i-1길이의 8로 시작하는 계단 수의 개수와 같습니다.
dp[i][9] = dp[i-1][8];
}3. 초기값 설정
초기값으로는 길이가 1일 때의 계단 수의 개수만 설정해주면 됩니다.
주의해야 할 점은, int형 범위를 넘을 수 있기 때문에 long 배열을 사용합니다.
for(int i=0; i<=9; i++) {
dp[1][i] = 1L;
}
🗝 전체 코드
import java.io.*;
import java.util.*;
public class Main {
static int N;
static final long MOD = 1_000_000_000L;
public static void main(String args[]) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(bf.readLine());
long[][] dp = new long[N+1][10];
// init
for(int i=0; i<=9; i++) {
dp[1][i] = 1L;
}
for(int i=2; i<=N; i++) {
// 0으로 시작하는 수의 개수
dp[i][0] = dp[i-1][1];
for(int j=1; j<=9; j++) {
// 9일경우는 이전 자릿수의 8로 시작하는 수의 개수와 동일하다!
if(j == 9) dp[i][9] = dp[i-1][8] % MOD;
// 나머지 수들은 이전 숫자의 j-1로 시작하는 수의 개수와 j+1로 시작하는 수의 개수를 더한 값이다.
else dp[i][j] = (dp[i-1][j-1] % MOD + dp[i-1][j+1] % MOD) % MOD;
}
}
long result = 0;
for(int i=1; i<=9; i++) {
result = (result + dp[N][i]) % MOD; // 정답을 더하면서 오버플로우가 발생할 수 있으므로 주의!
}
System.out.print(result);
}
}감사합니다!
반응형
