
안녕하세요, 알고리즘을 정리하는 포스팅입니다. 다른 알고리즘을 참고하시려면 해당 카테고리를 이용해주세요. 😊
'🌻 JAVA/알고리즘, 자료구조' 카테고리의 글 목록
공부한 것들 정리한 내용을 포스팅합니다.
iseunghan.tistory.com
분할 정복 (Merge Sort)
Merge Sort, 분할 정복, 병합 정렬, 합병 정렬 이라고도 한다. 시간복잡도는 최악의 상황까지도 O(n log n)을 보장한다.
나는 이 알고리즘을 공부할때, 분할 정복이라고 배워서 분할 정복이라고 칭하겠다.
그렇다면 왜 분할 정복일까?
Merge Sort가 O(n logn)을 보장할 수 있었던 이유는 정렬 할 배열을 반으로 분할 한뒤 각각 정렬 시키고 합치기 때문에 속도가 빠르다고 할 수 있다. (아래의 이미지를 보자)
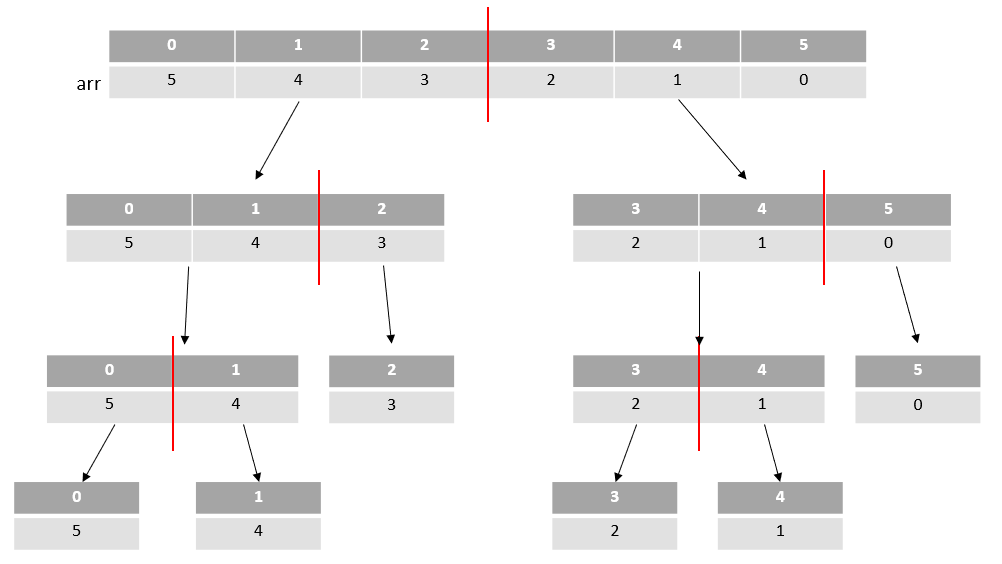
배열을 반으로 자르고, 그 자른 배열을 또 반으로 자르고, 그렇게 혼자가 될때까지 분할 시킨다.
뭔가 반복적인 과정이 보인다. 이 정렬은 재귀로 표현 할 수 있다.
각 처리 하는 순서를 번호로 표시 해봤다.
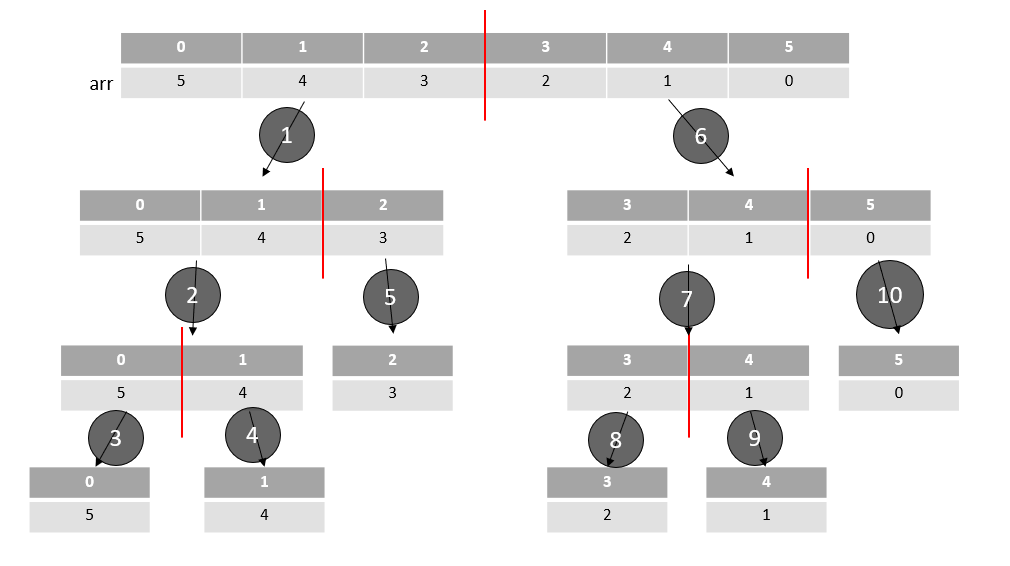
그럼 각 순서대로 처리 하는 과정을 살펴 보자.
- mergeSort(arr, 0, 5);
middle을 먼저 구한다. middle = (0 + 5) / 2 --> 2
그럼 두번 나눠서 재귀 호출을 한다.
- mergeSort(arr, 0, middle);
- mergeSort(arr, middle+1, 5);
- 1. mergeSort(arr, 0, 2);
int m = 0;
int n = 2;
int middle = (m+n) / 2; // 1
- mergeSort(arr, m, middle); // recursion (arr, 0, 1)
- mergeSort(arr, middle+1, n); // recursion (arr, 2, 2)
- 2. mergeSort(arr, 0, 1);
int m = 0;
int n = 1;
int middle = (m+n) / 2; // 0
- mergeSort(arr, m, middle); // recursion (arr, 0, 0)
- mergeSort(arr, middle+1, n); // recursion (arr, 1, 1)
- 3. mergeSort(arr, 0, 0);
int m = 0;
int n = 0;
int middle = (m+n) / 2; // 0
호출 할 필요가 없다!
- 4. mergeSort(arr, 1, 1);
int m = 0;
int n = 0;
int middle = (m+n) / 2; // 0
마찬가지로 호출 할 필요가 없다!
여기서 알 수 있는 조건 mergeSort 호출 시 m == n일 경우 호출 할 필요없다. ( m < n ) 인 경우만 호출하면 된다.
- 5. mergeSort(arr, 2, 2); -> 호출 X
- 6. mergeSort(arr, 3, 5);- > 3,4/5,5 호출
- 7. mergeSort(arr, 3, 4); -> 3,3/4,4 호출
- 8. mergeSort(arr, 3, 3); -> 호출 X
- 9. mergeSort(arr, 4, 4); -> 호출 X
- 10. mergeSort(arr, 5, 5); -> 호출 X
- 7. mergeSort(arr, 3, 4); -> 3,3/4,4 호출
자 여기까지 분할 하는 과정을 살펴보았는데, 코드로 나타내면 아래와 같다.
public void mergeSort(int[] arr, int m, int n) {
if(m < n) {
int middle = (m + n) / 2;
mergeSort(arr, m, middle);
mergeSort(arr, middle + 1, n);
}
}
이제 분할 정복에서 정복 과정, 즉 합치면서 정렬 시키는 과정을 살펴보자.
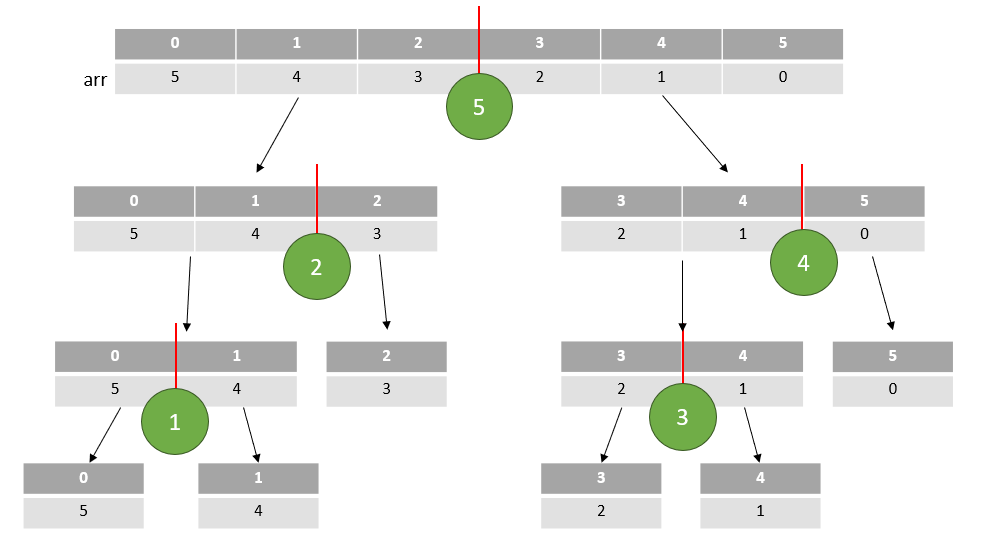
총 5번에 걸쳐서 정복 과정이 이루어 질텐데, 그 과정을 한번 하나씩 보겠다.
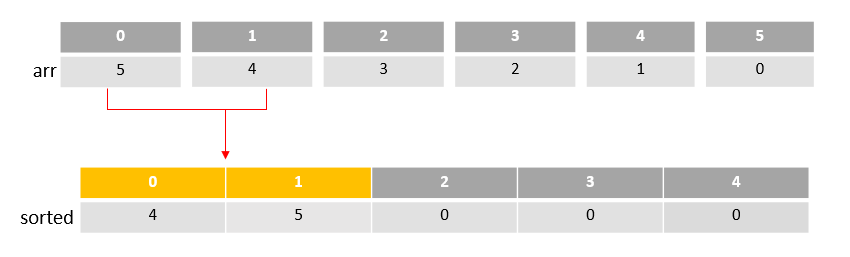
- 1. merge(arr, 0, 1)

인자 값으로 arr배열의 주소와, 시작 인덱스, 마지막 인덱스 를 넘겨준다.
각 인덱스의 값들을 비교하면서 sorted 배열에다가 넣는다.
- 2. merge(arr, 0, 2)
이제 지금이 중요하다. 앞에 정렬된 두개의 인덱스와 arr[2] 를 비교해서 sorted에 넣어야 하는데
앞에 배열은 이미 정렬된 상태이기 때문에, for문으로 비교후 sorted에 넣어주면 된다.

비교후 값을 넣어주고, 해줘야 할 것이 k값 증가, 넣은 인덱스 값 증가 시키기. 위에 그림은 k++, j++ 를 해주면 된다.
그치만, 조심해야 할것이 j++ 를 해주면 인덱스가 벗어나게 된다.
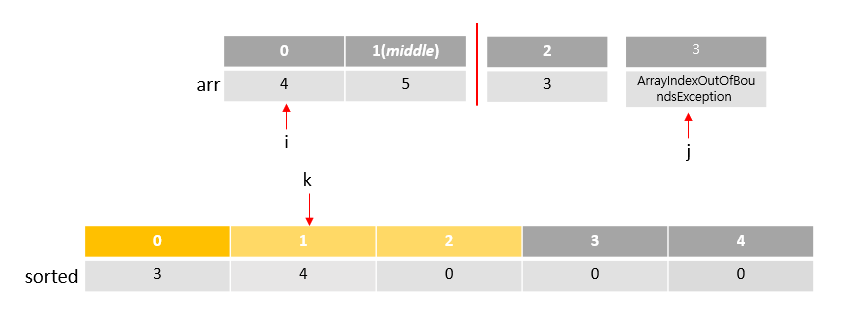
그래서 우리가 설정 해줘야 할 조건은 ( i <= middle && j <= n ) 이다.
코드로 작성해보면,
while (i <= middle && j <= n) {
if (a[i] < a[j]) {
sorted[k] = a[i];
i++;
}else{
sorted[k] = a[j];
j++;
}
k++;
}
자 그 다음 해야 할 것이 무엇일까?
while문이 종료되면, 아직 남아 있는 데이터가 있다는 뜻이다. 그와 동시에 한쪽은 이미 다 옮겼고, 나머지 한쪽만 반복문을 통해 넣어주기만 하면 된다.
코드로 함께 보자.
1. 만약 i가 middle보다 커졌을 경우
if(i > middle) {
for(int t = j; t <= n; t++) {
sorted[k++] = arr[t];
}
}
2. 만약 j가 n보다 커졌을 경우
if(j > n) {
for(int t = i; t <= middle; t++) {
sorted[k++] = arr[t];
}
}
그 다음에 sorted 배열을 다시 arr 배열로 덮어씌어 주면 된다!
for(int t=m; t <= n; t++) {
arr[t] = sorted[t];
}
전체 코드
public class Merge_Sort_Tutorial {
static int number = 8;
static int[] sorted = new int[8];
private static void merge(int[] a, int m, int middle, int n) {
int i = m;
int j = middle + 1;
int k = m;
// 두 배열 중 하나를 다 옮길 때 까지 반복
while (i <= middle && j <= n) {
if (a[i] < a[j]) {
sorted[k] = a[i];
i++;
}else{
sorted[k] = a[j];
j++;
}
k++;
}
// 남아있는 데이터 삽입
if (i > middle) {
for (int t = j; t <= n; t++) {
sorted[k] = a[t];
k++;
}
}else{
for (int t = i; t <= middle; t++) {
sorted[k] = a[t];
k++;
}
}
// 정렬된 배열을 삽입
for (int t = m; t <= n; t++) {
a[t] = sorted[t];
}
}
private static void mergeSort(int[] a, int m, int n) {
if (m < n) {
int middle = (m + n) / 2;
mergeSort(a, m, middle);
mergeSort(a, middle + 1, n);
merge(a, m, middle, n);
}
}
public static void main(String[] args) {
int[] array = {7, 1, 5, 5, 8, 9, 3, 2};
mergeSort(array, 0 , array.length-1);
for (int i : array) {
System.out.print(i + ", ");
}
}
}

안녕하세요, 알고리즘을 정리하는 포스팅입니다. 다른 알고리즘을 참고하시려면 해당 카테고리를 이용해주세요. 😊
'🌻 JAVA/알고리즘, 자료구조' 카테고리의 글 목록
공부한 것들 정리한 내용을 포스팅합니다.
iseunghan.tistory.com
분할 정복 (Merge Sort)
Merge Sort, 분할 정복, 병합 정렬, 합병 정렬 이라고도 한다. 시간복잡도는 최악의 상황까지도 O(n log n)을 보장한다.
나는 이 알고리즘을 공부할때, 분할 정복이라고 배워서 분할 정복이라고 칭하겠다.
그렇다면 왜 분할 정복일까?
Merge Sort가 O(n logn)을 보장할 수 있었던 이유는 정렬 할 배열을 반으로 분할 한뒤 각각 정렬 시키고 합치기 때문에 속도가 빠르다고 할 수 있다. (아래의 이미지를 보자)

배열을 반으로 자르고, 그 자른 배열을 또 반으로 자르고, 그렇게 혼자가 될때까지 분할 시킨다.
뭔가 반복적인 과정이 보인다. 이 정렬은 재귀로 표현 할 수 있다.
각 처리 하는 순서를 번호로 표시 해봤다.

그럼 각 순서대로 처리 하는 과정을 살펴 보자.
- mergeSort(arr, 0, 5);
middle을 먼저 구한다. middle = (0 + 5) / 2 --> 2
그럼 두번 나눠서 재귀 호출을 한다.
- mergeSort(arr, 0, middle);
- mergeSort(arr, middle+1, 5);
- 1. mergeSort(arr, 0, 2);
int m = 0;
int n = 2;
int middle = (m+n) / 2; // 1
- mergeSort(arr, m, middle); // recursion (arr, 0, 1)
- mergeSort(arr, middle+1, n); // recursion (arr, 2, 2)
- 2. mergeSort(arr, 0, 1);
int m = 0;
int n = 1;
int middle = (m+n) / 2; // 0
- mergeSort(arr, m, middle); // recursion (arr, 0, 0)
- mergeSort(arr, middle+1, n); // recursion (arr, 1, 1)
- 3. mergeSort(arr, 0, 0);
int m = 0;
int n = 0;
int middle = (m+n) / 2; // 0
호출 할 필요가 없다!
- 4. mergeSort(arr, 1, 1);
int m = 0;
int n = 0;
int middle = (m+n) / 2; // 0
마찬가지로 호출 할 필요가 없다!
여기서 알 수 있는 조건 mergeSort 호출 시 m == n일 경우 호출 할 필요없다. ( m < n ) 인 경우만 호출하면 된다.
- 5. mergeSort(arr, 2, 2); -> 호출 X
- 6. mergeSort(arr, 3, 5);- > 3,4/5,5 호출
- 7. mergeSort(arr, 3, 4); -> 3,3/4,4 호출
- 8. mergeSort(arr, 3, 3); -> 호출 X
- 9. mergeSort(arr, 4, 4); -> 호출 X
- 10. mergeSort(arr, 5, 5); -> 호출 X
- 7. mergeSort(arr, 3, 4); -> 3,3/4,4 호출
자 여기까지 분할 하는 과정을 살펴보았는데, 코드로 나타내면 아래와 같다.
public void mergeSort(int[] arr, int m, int n) {
if(m < n) {
int middle = (m + n) / 2;
mergeSort(arr, m, middle);
mergeSort(arr, middle + 1, n);
}
}
이제 분할 정복에서 정복 과정, 즉 합치면서 정렬 시키는 과정을 살펴보자.

총 5번에 걸쳐서 정복 과정이 이루어 질텐데, 그 과정을 한번 하나씩 보겠다.
- 1. merge(arr, 0, 1)

인자 값으로 arr배열의 주소와, 시작 인덱스, 마지막 인덱스 를 넘겨준다.
각 인덱스의 값들을 비교하면서 sorted 배열에다가 넣는다.

- 2. merge(arr, 0, 2)
이제 지금이 중요하다. 앞에 정렬된 두개의 인덱스와 arr[2] 를 비교해서 sorted에 넣어야 하는데
앞에 배열은 이미 정렬된 상태이기 때문에, for문으로 비교후 sorted에 넣어주면 된다.

비교후 값을 넣어주고, 해줘야 할 것이 k값 증가, 넣은 인덱스 값 증가 시키기. 위에 그림은 k++, j++ 를 해주면 된다.
그치만, 조심해야 할것이 j++ 를 해주면 인덱스가 벗어나게 된다.

그래서 우리가 설정 해줘야 할 조건은 ( i <= middle && j <= n ) 이다.
코드로 작성해보면,
while (i <= middle && j <= n) {
if (a[i] < a[j]) {
sorted[k] = a[i];
i++;
}else{
sorted[k] = a[j];
j++;
}
k++;
}
자 그 다음 해야 할 것이 무엇일까?
while문이 종료되면, 아직 남아 있는 데이터가 있다는 뜻이다. 그와 동시에 한쪽은 이미 다 옮겼고, 나머지 한쪽만 반복문을 통해 넣어주기만 하면 된다.
코드로 함께 보자.
1. 만약 i가 middle보다 커졌을 경우
if(i > middle) {
for(int t = j; t <= n; t++) {
sorted[k++] = arr[t];
}
}
2. 만약 j가 n보다 커졌을 경우
if(j > n) {
for(int t = i; t <= middle; t++) {
sorted[k++] = arr[t];
}
}
그 다음에 sorted 배열을 다시 arr 배열로 덮어씌어 주면 된다!
for(int t=m; t <= n; t++) {
arr[t] = sorted[t];
}
전체 코드
public class Merge_Sort_Tutorial {
static int number = 8;
static int[] sorted = new int[8];
private static void merge(int[] a, int m, int middle, int n) {
int i = m;
int j = middle + 1;
int k = m;
// 두 배열 중 하나를 다 옮길 때 까지 반복
while (i <= middle && j <= n) {
if (a[i] < a[j]) {
sorted[k] = a[i];
i++;
}else{
sorted[k] = a[j];
j++;
}
k++;
}
// 남아있는 데이터 삽입
if (i > middle) {
for (int t = j; t <= n; t++) {
sorted[k] = a[t];
k++;
}
}else{
for (int t = i; t <= middle; t++) {
sorted[k] = a[t];
k++;
}
}
// 정렬된 배열을 삽입
for (int t = m; t <= n; t++) {
a[t] = sorted[t];
}
}
private static void mergeSort(int[] a, int m, int n) {
if (m < n) {
int middle = (m + n) / 2;
mergeSort(a, m, middle);
mergeSort(a, middle + 1, n);
merge(a, m, middle, n);
}
}
public static void main(String[] args) {
int[] array = {7, 1, 5, 5, 8, 9, 3, 2};
mergeSort(array, 0 , array.length-1);
for (int i : array) {
System.out.print(i + ", ");
}
}
}
